Data Transformations
Choice depends on data set!
- Center and standardize
- Center: subtract from each value the mean of the corresponding vector
- Standardize: devide by standard deviation
- Result: Mean = 0 and STDEV = 1
- Center and scale with the
scale()function- Center: subtract from each value the mean of the corresponding vector
- Scale: divide centered vector by their root mean square (rms):
\(x_{rms} = \sqrt[]{\frac{1}{n-1}\sum_{i=1}^{n}{x_{i}{^2}}}\)
- Result: Mean = 0 and STDEV = 1
- Log transformation
- Rank transformation: replace measured values by ranks
- No transformation
Distance Methods
List of most common ones!
- Euclidean distance for two profiles X and Y:
\(d(X,Y) = \sqrt[]{ \sum_{i=1}^{n}{(x_{i}-y_{i})^2} }\)
- Disadvantages: not scale invariant, not for negative correlations
- Maximum, Manhattan, Canberra, binary, Minowski, …
- Correlation-based distance: 1-r
- Pearson correlation coefficient (PCC):
\(r = \frac{n\sum_{i=1}^{n}{x_{i}y_{i}} - \sum_{i=1}^{n}{x_{i}} \sum_{i=1}^{n}{y_{i}}}{ \sqrt[]{(\sum_{i=1}^{n}{x_{i}^2} - (\sum_{i=1}^{n}{x_{i})^2}) (\sum_{i=1}^{n}{y_{i}^2} - (\sum_{i=1}^{n}{y_{i})^2})} }\)
- Disadvantage: outlier sensitive
- Spearman correlation coefficient (SCC)
- Same calculation as PCC but with ranked values!
- Pearson correlation coefficient (PCC):
\(r = \frac{n\sum_{i=1}^{n}{x_{i}y_{i}} - \sum_{i=1}^{n}{x_{i}} \sum_{i=1}^{n}{y_{i}}}{ \sqrt[]{(\sum_{i=1}^{n}{x_{i}^2} - (\sum_{i=1}^{n}{x_{i})^2}) (\sum_{i=1}^{n}{y_{i}^2} - (\sum_{i=1}^{n}{y_{i})^2})} }\)
There are many more distance measures
- If the distances among items are quantifiable, then clustering is possible.
- Choose the most accurate and meaningful distance measure for a given field of application.
- If uncertain then choose several distance measures and compare the results.
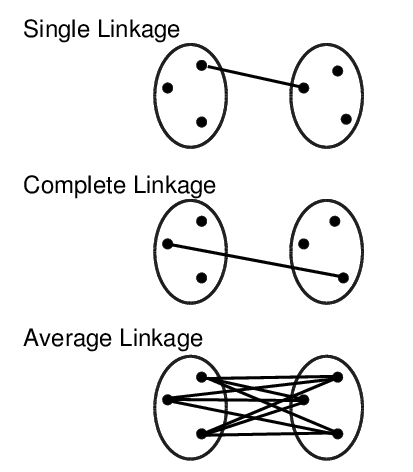
Cluster Linkage
 Previous Page Next Page
Previous Page Next Page
